MCS – 013(Discrete Mathematics) Important Short Notes| Expected Question |IGNOU BCA|

A course called MCS-013: Discrete Mathematics is part of the Bachelor of Computer Applications (BCA) curriculum offered by Indira Gandhi National Open University (IGNOU). For students who want to have a solid mathematical foundation—which is essential for computer science and its applications—this course is essential. An outline of the course, its organization, and its significance is given below:

Course Goals
The following are the main goals of the MCS-013 course:

• Describe the fundamental ideas of discrete mathematics.
• Develop your ability to reason logically and solve problems.
• lays the groundwork for later computer science and related topic courses.
• Give students the opportunity to use discrete mathematics in real-world data structure and computing scenarios.

Introduction to IGNOU BCA MCS-013: Discrete Mathematics

One of India’s top distance learning institutions, Indira Gandhi National Open University (IGNOU), provides a Bachelor of Computer Applications (BCA) program that aims to provide students with a thorough understanding of computer science and its applications. Among the program’s essential courses is MCS-013: Discrete Mathematics. This course is a fundamental building block that is necessary for students to acquire the reasoning and analytical abilities needed in a variety of computer science fields.

The study of mathematical structures that are essentially discrete rather than continuous is the domain of discrete mathematics. Discrete mathematics is concerned with discrete values, as opposed to continuous variables, which are the subject of calculus and analysis. This makes it especially relevant to computer science, because handling data frequently involves logical.

Understanding the Importance of MCS-013 Short Notes:

1. Overview : Brief notes reduce an extensive amount of material into essential ideas and points. They offer a rapid and effective means of studying the key subjects in advance of the examination.

2. Focus on the Essentials: You may focus on each topic’s key elements by summarizing the available information. This guarantees that you cover the most relevant subjects and helps in setting priorities for your study materials.

3. Improved Retention: Taking quick notes requires you to take an active role with the information. Compared to passive reading, active learning promotes improved understanding and retention of knowledge.

4. Quick Reference: Brief notes are a quick reference that come in helpful when making last-minute changes. To fast brush up on specific concepts or formulas, you can swiftly scan them.

5. Time management: You may cover a lot of ground in less time by taking brief notes. This is very helpful if you don’t have much time to study before the test.

Most Repeated MCS-012 Important Questions for IGNOU BCA Exams Semester Wise :

BLOCK 1

Ques.1 Truth Value :
p -> q Λ ~ r <-> r ⊕ q
3+5=2

Ques. 2 Equivalence:
p -> ( q -> p )
Ques. 3 Verify that p Λ q Λ ~ p is contradiction and p -> q <-> – p
V q is a tautology
~ ∀ P(x) Ξ ∃ x ~ P(x)

Ques. 4 Prove that if x^2 – 4 = 0 , then x not equal to by contradiction.

Ques. 5 Show that under root 2 is irrational.

Ques. 6 Mathematical Induction.

1 + 1/4 + 1/9+…. +1 / n ^ 2 <=2 -1/n
5 + 10 + 15 +…. + 5 n = 5 n ( n + 1 ) / 2

Ques. 7 If p and q are two propositions, then

show that ~ (p V q) Ξ ~ p ~ q

Ques. 8 Circuit

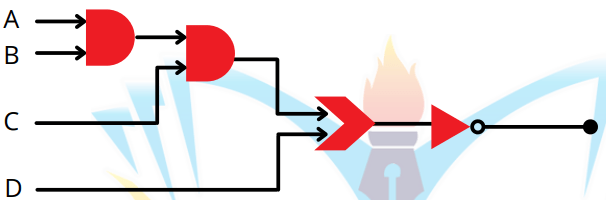
Ques. 9 Logic circuit

ox. y + x. y’ + x’ . y.

Ques. 10 Simpler Form
F (a, b, c) = (a’ Λ b’ Λ c’ ) V (a’ Λ b’ Λ c ) V (a Λ b Λ c’ )
X( x1, x2, x3) = (x1 Λ x2 Λ x3 ) V (X1 Λ X2) V (X2 Λ X3)

Ques. 11 Boolean expression
What is dual of a Boolean expression. Explain
the principle of duality with the example
(x + y’+ z’) (xy + x’z)

Ques.1 Venn Diagram :
A Π B Π C
A Π B – C

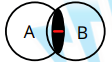
Find the dual of A U (B U C)

Ques. 2 Given S = (1, 2,… , 10) and a Relation R on S where R= {(x, y)| x + y = 10}

Ques. 3 Given A={ 1, 2, 3, 4 } and Relation R as { ( 1, 1 ), ( 1, 2 ),
( 1, 3 ), ( 1, 4 ), }

Ques. 4 Where r has the following properities or not ?

Reflexive , Transitive and Symmetric
If f: f R -> R is a function such that f(x)=3x+2, prove that f is
one – one ratio.

Ques. 5 Find the f inverse of the function

f ; f( x ) = x ^ 3 – 3
f i. e. , f ^ 1

BLOCK 2

Ques. 6 Let f be a permutation function defined as follows :

• f ( 1 ) = 2, f ( 2 ) = 4, f ( 3 ) = 1, f ( 4 ) = 3

Ques. 7 Distinguishable words can framed in letters

• MISSISSPPI
• PERMUTATION

Ques. 8 Explain Pascal’s Triangle.

Ques. 9 Probability

Two dice, one red and one white, are rolle.

Ques. 10 State Pigeonhole principle.

Ques. 11 What is the probability that a number between 1 and
200 is divisible by neither 2, 3, 5 nor 7.

Download PDF Of Above Content In 3 Paper

Read More: MCS – 012(COMPUTER ORGANISATION & ASSEMBLY LANGUAGE) Important Short Notes| Expected Question |IGNOU BCA|

Conclusion:

With these IGNOU MCS-012 BCA short notes, you’ll be well-equipped to tackle your exams with confidence. Remember to complement your study efforts with regular practice and mock tests. Good luck!